Voy a continuar explicando qué más cosas se pueden hacer si construyes unas piezas extras para los Pattern Blocks con la plantilla que hemos creado en reseteo matemático. Si aun no sabéis cómo hacer las piezas, leed Pattern Blocks low-cost, donde doy ideas y consejos para fabricarlas.
También puedes leer la entrada anterior de actividades con las piezas extra de los Pattern Blocks:
En la última entrada sólo utilicé los polígonos regulares y la característica de tener las piezas de varios colores. Hoy explicaré de dónde salen las distintas piezas rectangulares y triangulares y cómo trabajar con ellas.
Antes de meterme con las explicaciones sólo quiero recordaros que todas las piezas extra tienen al menos uno de los lados de la misma longitud que las piezas normales de los Pattern Blocks, así que podéis utilizarlas con ellos sin problemas, o usarlos sólo para inventar diseños nuevos si queréis.
Triángulos y rectángulos a partir del cuadrado
El primer grupo de piezas son los triángulos y rectángulos que se crean al partir el cuadrado por la mitad o en 4 partes.
Si cortáis un cuadrado por la mitad de dos de sus lados, obtenéis dos rectángulos de área 1/2.
Por otro lado, si en lugar de partir el cuadrado por la mitad de sus lados lo hacemos por 2 vértices no consecutivos, tenemos 2 triángulos de área 1/2. Al repetir la operación con los otros dos vértices tenemos 4 cuadrados de área 1/4.
Estas nuevas piezas se pueden utilizar para trabajar las fracciones de igual forma que con los Pattern Blocks normales, la única novedad es que ahora disponemos de la fracción 1/4.

Por ejemplo, en la foto de arriba además de ver las distintas piezas, se está trabajando el concepto de fracciones equivalentes.
También se pueden utilizar para hacer sumas de fracciones, aunque solo tienes disponibles 1/2 y 1/4. Esto limita bastante pero puede ser una ventaja si lo que quieres es introducir el concepto de fracción a niños pequeños.
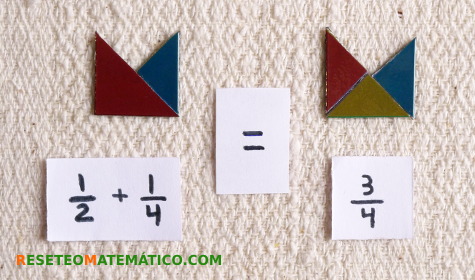
Triángulos a partir del triángulo equilátero
En segundo lugar tenemos los triángulos que se crean al partir un triángulo equilátero por la mitad. Los triángulos que obtenemos tienen 1/2 el área del triángulo equilátero.

Gracias a este nuevo triángulo se amplía mucho la cantidad de operaciones con fracciones que podemos hacer con los Pattern Blocks. Si consideramos el hexágono como unidad, ahora podemos trabajar con la fracción 1/12.

Como más arriba ya he puesto imágenes de como trabajar la equivalencia de fracciones y un ejemplo de suma, voy a poneros una multiplicación de una fracción por un entero para que veáis que también se pueden hacer de forma manipulativa.

Triángulos a partir del pentágono
El pentágono es un polígono bastante especial. Encierra en su interior una proporción entre distintos elementos que lo componen que es conocida como relación áurea o número de oro. Esta proporción se repite mucho en la naturaleza y se ha usado a lo largo de la historia en el arte relacionado con la divinidad.
No voy a soltaros el rollo explicando en qué consiste este número áureo, pero es el responsable de que los triángulos que se forman partiendo el pentágono por sus diagonales den tanto juego a la hora de construir con ellos.

Me cuesta mucho explicar cómo se forman los distintos triángulos que forman parte de este grupo de piezas, sobre todo porque se pueden generar de varias maneras. En la imagen de abajo podéis ver que el triángulo amarillo se puede formar trazando dos diagonales del pentágono y también prolongando dos lados del pentágono no consecutivos.

Así que lo mejor es que os hagáis las piezas y descubráis montones de relaciones y sorprendentes modelos que se pueden hacer con ellos. Si te gusta la geometría te puedes pasar horas jugando.

Clasificar los tipos de triángulos
Con tantos triángulos a vuestra disposición, tenéis al menos un triángulo de cada tipo. Podéis clasificar los triángulos según la longitud de sus lados.

O también según la amplitud de sus ángulos.

Y con esto acabo de explicar todas las actividades que te permiten hacer las piezas extra de Pattern Blocks y que no puedes hacer con los bloques geométricos normales. Por supuesto, con ellos puedes hacer además todas las actividades que expliqué en la entrada de Pattern Blocks o bloques geométricos.
Si conocéis alguna actividad más o no he explicado suficientemente bien algún punto, ponédmelo en los comentarios. Y si os ha gustado, compartid.





Deja una respuesta