Esta semana tenemos un nuevo post con ideas para trabajar con los Policubos. Así que olvida la idea de que los Policubos son solo para educación infantil, porque esta semana trabajaremos sobre todo con conceptos que se ven en educación secundaria.
Te recuerdo nuestras anteriores entradas sobre Policubos:
También puedes visitar nuestro tablero de Pinterest con enlaces a plantillas gratuitas de otras personas para hacer las actividades con Policubos de todo tipo.
Estadística: construir diagramas de barras.
La estadística se dedica a clasificar y hacer recuento de todos los hechos que tienen una característica en común, para poder llegar a conclusiones.
Estos datos que se recogen se pueden mostrar en una tabla, o de forma más visual en una gráfica.
Con los Policubos, podemos construir una gráfica de barras con niños pequeños, que les ayude a entender la relación entre la gráfica y la realidad.
Se puede construir un diagrama colocando un Policubo cada día en la columna correspondiente según el clima que haga.
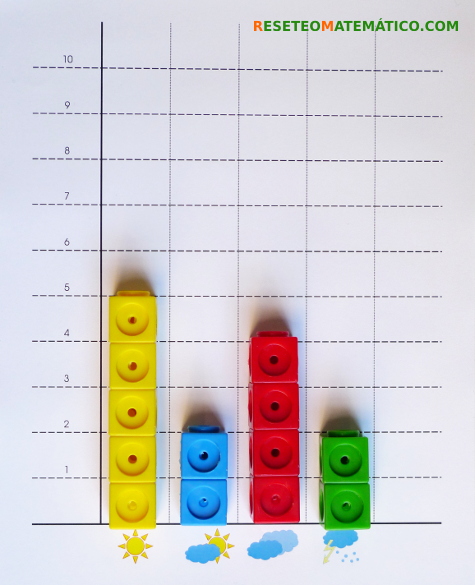
Después de unos cuantos días se pueden analizar los datos: ¿Ha habido más días de sol que de lluvia? ¿Cuantos días ha estado nublado?
Si no tienes tanto tiempo como para hacer un estudio del clima, puedes construir la gráfica de las frutas favoritas de los niños o su color de pelo. Seguro que se te ocurren un montón de ideas.
Combinatoria
La Combinatoria es la parte de las Matemáticas que busca procedimientos y estrategias para contar distintas formas de agrupar elementos de un conjunto.
Según las reglas que se utilicen para agrupar determinado número de elementos se distinguen 3 tipos:
- Permutaciones: se utilizan todos los elementos una vez y es importante el orden.
- Combinaciones: no se utilizan todos los elementos ni importa el orden.
- Variaciones: no se utilizan todos los elementos pero sí importa el orden.
Se pueden hacer actividades de cualquiera de los tipos de agrupaciones de elementos.
La mejor manera de trabajar la combinatoria con Policubos es plantear actividades de investigación. Lanzas una pregunta y pides que encuentren todas las posibles opciones. Cuanto más abierta sea la propuesta, más fácil es que todo el mundo encuentre una manera propia de trabajar.
Después se puede intentar encontrar una manera de calcular cuantas agrupaciones hay sin tener que construirlas.
A continuación voy a poner algunos ejemplos de investigaciones que se pueden proponer.
Permutaciones según color
Vamos a construir una barra con 8 cubos, 4 de cada color. ¿De cuantas formas pueden hacerse?

Las variaciones se pueden trabajar de forma similar. Si una vez hecho este ejercicio descartamos las piezas que son iguales pero giradas, ¿cuántas formas diferentes tenemos de construir la barra?

Es interesante que cada grupo de trabajo explique que estrategia ha utilizado para encontrar todos los resultados. Normalmente te sorprendes porque a alguien se le ocurre hacerlo de alguna forma que no habías imaginado.
De este tipo de ejercicio se pueden hacer miles de variaciones:
- ¿De cuantas formas podemos unirlas si la barra es de 8 cubos, 4 de cada color?
- ¿Y si la barra es de 8 cubos, 3 de un color y 5 de otro?
- ¿Y con 2 de un color y 6 de otro?
- ¿Y si la barra es de 9 cubos y tenemos 3 piezas de 3 colores distintos?…
Variaciones por la colocación espacial
En lugar de construir barras, vamos a aprovechar que los Policubos se pueden unir por cualquiera de sus caras y buscar otras figuras que se pueden construir.
¿Cuantas piezas diferentes se pueden crear uniendo 4 cubos?

Un ejemplo de este tipo de ejercicio es el pentominó del que hablamos en el apartado de juegos y puzles. El Pentominó está formado por las 12 piezas distintas que se forman al unir 5 cuadrados por sus lados.

Pero si no unimos solo las piezas en plano ¿Cuantas piezas nuevas obtenemos? No lo sé porque no lo he calculado, pero puedes intentar descubrirlo 😉
Si quieres complicar mucho más el ejercicio, puedes introducir las 2 variables, número de piezas y color. Por ejemplo, intentar calcular cuantas piezas se pueden hacer uniendo 6 cubos de dos colores diferentes (3 cubos de cada color) por cualquiera de sus caras.
Probabilidad
Cuando se realizan Variaciones y combinaciones, no todas las opciones tienen la misma probabilidad de ocurrir. Algunas pasan más a menudo que otras.
Esto es algo que se comprende bastante bien cuando se ve en un ejemplo práctico, pero que resulta muy engorroso que cuando te lo explican de forma teórica.
Así que vamos a empezar a trabajarlo de forma práctica. Planteamos una situación, hacemos varios ensayos y apuntamos los resultados.
La situación puede ser sacar 2 cubos de una bolsa que tiene la mitad de cubos de un color y la mitad de otro. O sacar 3 cubos de una bolsa donde ¼ son de un color y ¾ son de otro. Este tipo de problemas normalmente aparece en los libros de texto pero a casi nadie se le ocurre hacerlo in situ a ver que pasa.
Tras acabar con los ensayos, se pueden comentar los resultados e ir introduciendo conceptos teóricos:
- ¿Son todos los sucesos igual de probables?
- ¿Hay algún suceso seguro?
- ¿Hay algún suceso imposible?
Para los que no sepáis que es un suceso seguro y uno imposible lo explico brevemente con un ejemplo. Si tengo una bolsa con cubos rojos y saco uno, el que saque un cubo rojo es un suceso seguro (pasa siempre), pero que salga un cubo azul es un suceso imposible (no puede pasar nunca).
Por último se puede intentar traducir la probabilidad a una formula numérica. Las probabilidades de que ahora lo entiendan son mayores.
Las posibilidades de trabajar estadística y combinatoria con Policubos son enormes.
Como puedes ver, se pueden plantear actividades muy sencillas o súper complejas. Puedes adaptarla las actividades a un determinado nivel o mejor aún hacer una actividad muy abierta para que personas puedan trabajarla a la vez a distintos niveles.
Si quieres seguir aprendiendo de Policubos, puedes mirar las otras entradas que he escrito sobre el tema. Aquí tienes los enlaces:
- Qué son y para qué sirven
- Geometría y visualización espacial
- Actividades de lógica
- Juegos y puzles 3D
- Introducción al concepto de número





Deja una respuesta