Proyecto Caja Abierta: Multinivel

Título: Caja Abierta

Edades: 8-108                                              Temporalización: 5 – 6 sesiones

Conceptos: longitud, volumen, unidades de volumen, capacidad    (Quizá: gráficas, funciones, optimización, derivadas, derivadas sucesivas)

Material: papel blanco, papel cuadriculado en centímetros, tijeras, celo, regletas unidad

Inauguro con esta entrada la sección Matemáticas por Proyectos donde encontrarás proyectos multinivel de  investigación, manipulación, discusión y colaboración. Como verás otra forma de trabajar las matemáticas.

¿Te gustaría trabajar  con un proyecto en el que aparezcan conceptos geométricos como longitud, volumen (y sus unidades), capacidad, y quizá también, pero no obligatoriamente, otros aspectos matemáticos, como dependencia funcional, maximización y representaciones gráficas?

Si te animas a embarcarte en este proyecto, ten en cuenta que la información relevante está dividida en tres entradas.                                 En esta primera doy una somera descripción del proyecto y a continuación me centro en su carácter multinivel.

La siguiente entrada, titulada Proyecto Caja Abierta: Manos a la Obra incluye las distintas fases del proyecto, con los imprimibles (hoja de trabajo, evaluación) para llevarlo a cabo.

Por último, en la tercera y última entrada de la serie, titulada Proyecto Caja Abierta: Manipulativo  os propondré una forma de incluir la manipulación en el proyecto.

 Construcción de la caja

En la imagen puedes ver cómo se monta el tipo de caja sin tapa con el que vamos a trabajar.

Empieza con un cuadrado de papel o cartulina de 15 cm de lado. Recorta cuatro cuadraditos iguales en las cuatro esquinas.  Pliega  dejando una base cuadrada. Une los lados de los rectángulos con celo para que estos hagan de paredes de la caja. Ya tienes una de tus cajas sin tapa.

Trabajo para los estudiantes

Las instrucciones para dar a los estudiantes se podrían escribir así:

 Partimos de un cuadrado de 15 cm de lado.

¿Cómo cambia la capacidad de la caja abierta que formamos a partir de él, según el lado del cuadrado pequeño que recortamos en cada esquina va creciendo?

Trabajad en grupos y haced un póster con vuestras conclusiones representándolas  visualmente mediante dibujos, tablas, gráficas…

Preparad argumentos para convencer a los demás de que vuestras conclusiones son válidas.

Puedes conseguir ya aquí la hoja de trabajo en formato pdf.

Agrupamientos

Recomiendo que los grupos sean de tres estudiantes. Y si fuera necesario, alguno de cuatro.

Para mi lo ideal es que los grupos incluyan estudiantes con diferentes niveles de motivación, de ambos sexos y  con distintas formas de  afrontar los problemas matemáticos. Quiero decir, una persona que  sigue más las estrategias aprendidas y lo calcula todo pacientemente se beneficiará de trabajar con otro que tira más de intuición y hace estimaciones . Y viceversa.

Temporalización

Alrededor de cinco sesiones.                                                                                             Puede parecer mucho a priori. Sin embargo, si das realmente tiempo a los alumnos para investigar (incluso manipular) necesitarán unas dos sesiones.  Si además llevas a cabo  las fases del proyecto que detallo en la siguiente entrada (confección de póster, discusión, puesta en común y evaluación) comprobarás que unas cinco sesiones son necesarias para todo el proyecto.

Edades

De 8 a 108 años de edad.                                                                                                 No es del todo una broma ya que este proyecto permite muy diferentes desarrollos. Puede ser trabajado a nivel de  primaria,  secundaria, bachillerato y, por supuesto, con adultos.  Encontrarás la explicación en el siguiente apartado.

Multinivel

Digo que este proyecto es multinivel porque, desde mi punto de vista, permite que personas de diferentes edades y diferentes experiencias previas con las matemáticas puedan avanzar en su aprendizaje.

Para explicarte el párrafo anterior te propongo un juego. Te propongo que te pongas en el lugar de esa profesora con estudiantes de entre 8 y 108 años. Ella presenta este proyecto y ¿qué enfoques diferentes aparecerían? ¿Qué trabajos diferentes harían los distintos grupos?

Describo a continuación algunos de ellos.

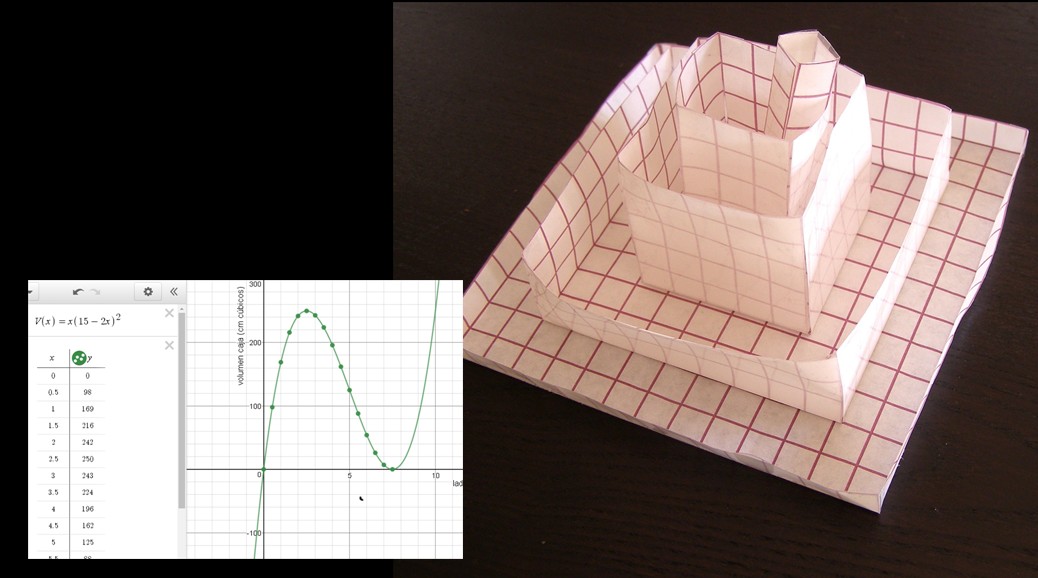
Manipulativo

Estudiantes que hacen el estudio manipulativo de las cajas de recortes 1×1, 2×2, 3×3 cm y llegan a la conclusión de que el volumen crece según el recorte aumenta de tamaño.   Expresan  sus conclusiones visualmente con fotografías.

Otros que montan unas cuantas cajas, e imaginan cómo serían las demás y concluyen que el volumen crece hasta que el recorte es de 3×3 cm y que disminuye según el recorte sigue creciendo.

Estudio exhaustivo de casos

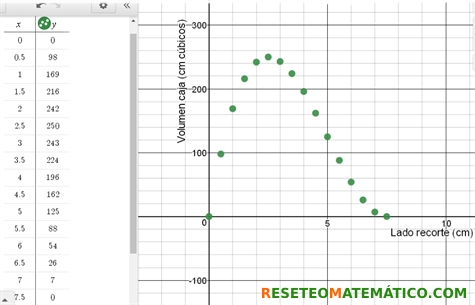
Grupos que no manipulan y que trabajan con dibujos. E incluyen en  su estudio los casos en los que recortamos cuadraditos de 0.5 cm, 1.5 cm, 2.5 cm … de lado.  Su conclusión es que el volumen es máximo para el recorte de 2.5 cm.

Representación gráfica

Otros que hacen el estudio del punto anterior y además, para representar visualmente sus descubrimientos utilizan una tabla y una gráfica. Las que muestro aquí están elaboradas con desmos.com.

Algebraico

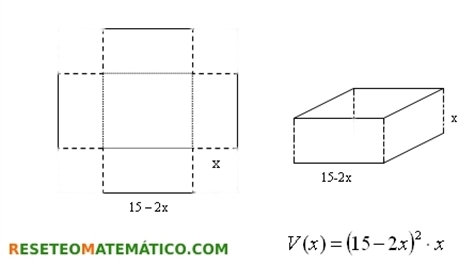
Estudiantes que identifican que en esta situación varía el lado del recorte y usan un símbolo (puede ser x u otro cualquiera) para referirse a cualquiera de sus valores. Identifican también que según varía el lado del recorte, x, varía también el volumen de la caja  y usan un símbolo (por ejemplo V) para referirse a cualquiera de los valores del volumen. Y escriben las operaciones que hay que hacer con x para obtener V. Es decir, la fórmula del volumen en función de x.

Y lo representan gráficamente.

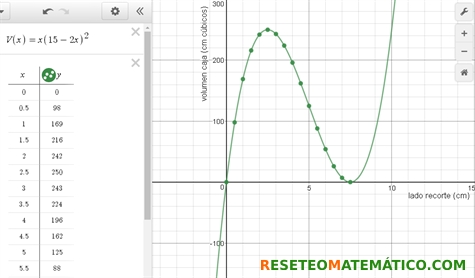
Para mostrar a un grupo estos dibujos y gráficas utiliza este fichero para proyectar en formato pdf.

Derivadas

Estudiantes que además de hallar la expresión algebraica del volumen, conocen el significado de la derivada y lo aplican para hallar el máximo de la función volumen así como sus intervalos de crecimiento y de decrecimiento.

Derivadas sucesivas

Grupos que comprenden el significado  de las derivadas sucesivas, hallan la derivada segunda de la función volumen para demostrar que, efectivamente, con un recorte de 2.5×2.5 cm, el volumen es máximo y no mínimo y con un recorte de 7.5×7.5 cm, el volumen es mínimo y no máximo.

Claro que esta situación es imposible. Nadie se enfrenta a un grupo con tantos niveles diferentes, ¿o sí?

Reflexión

Aquí van dos preguntas más para la reflexión:                                                 ¿Crees que alguno de estos grupos ha aprendido poco con su trabajo de investigación?                                                                                                                         ¿Piensas que habrían aprendido más si se les hubiera negado la posibilidad de manipulación, o la posibilidad de explorar casos concretos, y se hubiera obligado a todos los grupos a realizar el estudio algebraico? 

Gracias a

• Investigando las Matemáticas.  Libro 4. Robert Fisher y Alan Vince,1990. Ediciones AKAL. ISBN 84-7600-577-6. Página 41.
• Alberto Velasco (I.E.S. Galileo Galilei  Alcorcón). Suya fue la idea de ampliar el  proyecto que aparece en el libro arriba referido  hasta incluir el desarrollo algebraico (función volumen y derivadas).
• Map.mathshell.org, por las fases del proyecto y los ejemplos de evaluación para el aprendizaje.
• desmos.com, por su interfaz de fácil uso para realizar tablas y gráficas online.
• Jo Boaler, por su curso online de Stanford  How to Learn Math, en especial por su paradigma de la capacidad matemática en desarrollo.